 |  |
|  | |||||||
| Department of Basic Sciences The Department of Basic Sciences strives to maintain high standards of teaching in various branches specially Applied Mathematics. |
 |
| | Thread Tools | Search this Thread | Rate Thread | Display Modes |
|
#1
| ||||
| ||||
| Tangential annular flow between two coaxial rotating cylinders Problem. Consider an incompressible isothermal fluid in laminar flow between two coaxial cylinders, whose inner and outer wetted surfaces have radii of kR and R, respectively. The inner and outer cylinders are rotating at angular velocities Wi and Wo, respectively. End effects may be neglected. 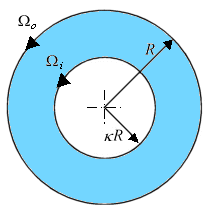 Figure. Tangential annular flow between two slowly rotating cylinders. a) Determine the steady-state velocity distribution in the fluid (for small values of Wi and Wo). b) Find the torques acting on the two cylinders during the tangential annular flow of a Newtonian fluid. Solution. Step. Simplification of continuity equation In steady laminar flow, the fluid is expected to travel in a circular motion (for low values of Wi and Wo). Only the tangential component of velocity exists. The radial and axial components of velocity are zero; so, vr = 0 and vz = 0. For an incompressible fluid, the continuity equation gives 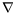 .v = 0. .v = 0. In cylindrical coordinates,  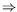 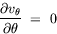 (1) (1) So, vq = vq (r, z). If end effects are neglected, then vq does not depend on z. Thus, vq = vq (r). Step. Simplification of equation of motion There is no pressure gradient in the q-direction. The components of the equation of motion simplify to 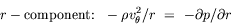 (2) (2) 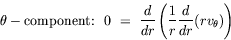 (3) (3) 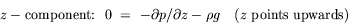 (4) (4) The r-component provides the radial pressure distribution due to centrifugal forces and the z-component gives the axial pressure distribution due to gravitational forces (the hydrostatic head effect). Step. Velocity profile by solving differential equation The q-component of the equation of motion is integrated to get the velocity profile: 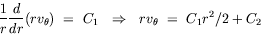 (5) (5) 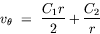 (6) (6) The no-slip boundary conditions at the two cylindrical surfaces are 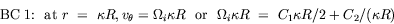 (7) (7) 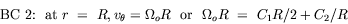 (8) (8) The integration constants are thus given by 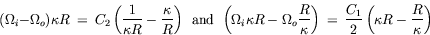 (9) (9) On substituting for C1 and C2, the velocity profile is obtained as 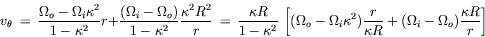 (10) (10) The velocity distribution given by the above expression can be written in the following alternative form: 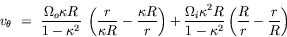 (11) (11) In the above form, the first term on the right-hand-side corresponds to the velocity profile when the inner cylinder is held stationary and the outer cylinder is rotating with an angular velocity Wo. This is essentially the configuration of the Couette - Hatschek viscometer for determining viscosity by measuring the rate of rotation of the outer cylinder under the application of a given torque (as discussed below). The second term on the right-hand-side of the above equation corresponds to the velocity profile when the outer cylinder is fixed and the inner cylinder is rotating with an angular velocity Wi. This is essentially the configuration of the Stormer viscometer for determining viscosity by measuring the rate of rotation of the inner cylinder under the application of a given torque (as discussed next). b) Step. Determination of momentum flux From the velocity profile, the momentum flux (shear stress) is determined as 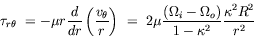 (12) (12) Step. Determination of torque The torque is obtained as the product of the force and the lever arm. The force acting on the inner cylinder itself is the product of the inward momentum flux and the wetted surface area of the inner cylinder. Thus, 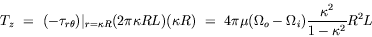 (13) (13) Similarly, the torque acting on the outer cylinder is obtained as the product of the outward momentum flux, the wetted surface area of the outer cylinder, and the lever arm. Thus, 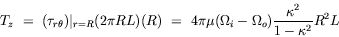 (14) (14) The tangential annular flow system above provides the basic model for rotational viscometers (to determine fluid viscosities from measurements of torque and angular velocities) and for some kinds of friction bearings.
__________________  |
 |
| Tags |
| annular, coaxial, cylinders, flow, rotating, tangential |
« Previous Thread
|
Next Thread »
| Currently Active Users Viewing This Thread: 1 (0 members and 1 guests) | |
| |
 Similar Threads
Similar Threads | ||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Plans for first rotating tower in Dubai (Dynamic Twisted Building) | .BZU. | Youtube Videos/Clips etc | 0 | 05-11-2010 01:37 AM |
| When tears flow in your eyes... | usman_latif_ch | Quotes | 1 | 20-04-2010 10:45 PM |
| Dubai's rotating tower; Preview of World's First Rotating Skyscraper | .BZU. | Technology | 0 | 23-03-2010 04:24 AM |
Almuslimeen.info | BZU Multan | Dedicated server hosting
Note: All trademarks and copyrights held by respective owners. We will take action against any copyright violation if it is proved to us.
All times are GMT +5. The time now is 02:01 PM.
Powered by vBulletin® Version 3.8.2
Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.
Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.

 bonfire
bonfire





 Linear Mode
Linear Mode

