 |  |
|  | |||||||
| Differential Equations and Linear Algebra Lectures by Sir Fazil |
 |
| | Thread Tools | Search this Thread | Rate Thread | Display Modes |
|
#1
| ||||
| ||||
|
In mathematics, a matrix (plural matrices) is a rectangular table of elements (or entries), which may be numbers or, more generally, any abstract quantities that can be added and multiplied. Matrices are used to describe linear equations, keep track of the coefficients of linear transformations and to record data that depend on multiple parameters. Matrices are described by the field of matrix theory. They can be added, multiplied, and decomposed in various ways, which also makes them a key concept in the field of linear algebra. Mathematical definition: An  matrix matrix  is a function is a function  where where  is any non-empty set. is any non-empty set.  is the Cartesian product of sets is the Cartesian product of sets  and and  We say that matrix 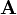 is a matrix over the set is a matrix over the set  . Important thing to note is that, if we want to have matrix algebra, the set . Important thing to note is that, if we want to have matrix algebra, the set  must be a ring and matrix must be a ring and matrix 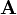 must be a square matrix (see Square matrices and related definitions below for further explanation). Since the set of all square matrices over a ring is also a ring, matrix algebra is usually called matrix ring. must be a square matrix (see Square matrices and related definitions below for further explanation). Since the set of all square matrices over a ring is also a ring, matrix algebra is usually called matrix ring.Since this article mainly considers matrices over real numbers, matrices shown here are actually functions  For Example The matrix  or or  is a is a  matrix. The element a2,3 or matrix. The element a2,3 or  is 7. In terms of the mathematical definition given above, this matrix is a function is 7. In terms of the mathematical definition given above, this matrix is a function  and, for example, and, for example,  and and  The matrix  is a is a 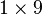 matrix, or 9-element row vector. matrix, or 9-element row vector.Square matrices: A square matrix is a matrix which has the same number of rows and columns. 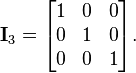
__________________ (¯`v´¯) `*.¸.*` ¸.*´¸.*´¨) ¸.*´¨) (¸.*´ (¸.Bzu Forum  Don't cry because it's over, smile because it happened Don't cry because it's over, smile because it happened  |
|
#2
| ||||
| ||||
|
matrix like we study in Matric or FSc(Preengeniering)if u DONE  |
 |
| Tags |
| algebra, linear, matrix |
« Previous Thread
|
Next Thread »
| Currently Active Users Viewing This Thread: 1 (0 members and 1 guests) | |
| |
 Similar Threads
Similar Threads | ||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Chapter 13: Linear-Digital ICs | bonfire | Electrical Circuits | 0 | 19-03-2011 08:09 PM |
| Program to find the sum of each row & column of a matrix of size n x m and if matrix is square, find the sum of the diagonals | bonfire | Object Oriented Programming | 0 | 09-03-2011 12:01 AM |
| Dutch Linear Clock.. | Raheel | ETC | 4 | 13-05-2010 12:39 AM |
| Linear combination of two vectors | .BZU. | Differential Equations and Linear Algebra | 4 | 07-10-2008 03:58 PM |
| Linear Algebra; Test Date | shmsa | Differential Equations and Linear Algebra | 6 | 25-09-2008 05:24 PM |
Almuslimeen.info | BZU Multan | Dedicated server hosting
Note: All trademarks and copyrights held by respective owners. We will take action against any copyright violation if it is proved to us.
All times are GMT +5. The time now is 01:28 AM.
Powered by vBulletin® Version 3.8.2
Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.
Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.

 .BZU.
.BZU.





 shmsa
shmsa


 Linear Mode
Linear Mode

